摘要
本文拟解决基于 “带有不可靠标签的数据” 训练神经网络的问题。
基于假设观察到的标签是真实标签的带噪观测结果,从而引入一个额外的噪音层,模拟噪音分布对真实标签的影响。
- 提出一种同时学习神经网络参数和噪声分布的方法
- 在几个标准分类任务上的对比实验说明了该方法对性能的提升。
- 在某些情况下,即使“人工手动标注并假定没有错误的数据”,该方法也有所帮助。
模型
假设在训练过程中不能直接观察到正确标签y,只能观察到带噪标签z
噪音分布可以看作关系标签间的转移概率
$\theta (i,j) = p(z=j|y=i) $
观测的带噪标签 z 的概率:
$ p(z=j|x;\omega, \theta) = \sum\limits_{i=1}^k p(z=j|y=i; \theta) p(y=i|x;\omega), $
$\omega是参数集合, x是输入特征(可以是句子、手工创建的特征等), k是关系的个数$
模型结构图如下:
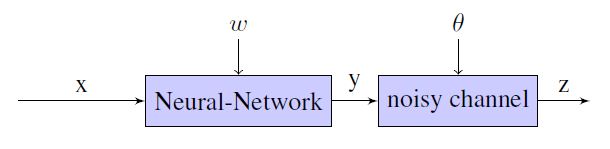
对于输入特征 $x$ , 编码后的特征向量表示为 $h = h(x)$,
$p(y=i|x;\omega) = \frac {\exp(u_i^\top h)}{\sum\limits_{j=1}^k \exp(u_j^\top h)}, i=1,2,…,k$
$u$ 是参数
训练阶段
给定 n 个输入特征 $x_1,…,x_n$, 相对应的观测带噪标签 $z_1,…, z_n$ , 真实标签 $y_1,…,y_n$
对数极大似然估计:
$L(\omega, \theta) = \sum\limits_{t=1}^n \log (\sum\limits_{i=1}^k p(z_t|y_t=i;\theta) p(y_t=i|x_t;\omega))$
目标是:最大化该似然函数,找出参数 $\omega$ 、噪音分布 $\theta$
由于
Improving Long-Tail Relation Extraction with Collaborating Relation-Augmented Attention