摘要
现有工作很少能够较好地解决关系三元组的重叠问题(overlapping triple problem)。
本文用一个新的视角来重新审视关系提取任务,并提出了一种级联二分标注框架(Cascade Binary Tagging Framework, 简称CasRel)。
该框架将关系(relation)建模为主体(subject)与客体(object)的函数映射,而不是像以前的工作那样将关系视为离散标签。
实验表明,该框架在多个场景下均可以获得性能提升,某些场景大幅度超越现有SOTA。
拟解决问题
重叠三元组问题overlapping triple problem有以下三种情形:

本文方案
本文关系抽取任务定义
本文的框架将关系(relation)建模为主体(subject)与客体(object)的函数映射,而不是像以前的工作那样将关系视为离散标签。
由学习关系分类器(relation为离散关系标签)
$f(s,o) \to r$
转变为学习主体s在关系r下对客体o的函数映射
$f_r(s) \to o$
基于上述视角,关系抽取任务可以分为以下两个步骤:
- 确定句子中所有可能的主体 (subject);
- 针对每个主体subject,使用特定于关系的标注器(relation-specific tagger)同时识别所有可能的关系和相应的客体object
CasRel框架(三部分):
BERT-based encoder module (基于Bert的编码器模块)
subject tagging module(主体标注模块)
relation-specific object tagging module(区分关系的客体标注模块)
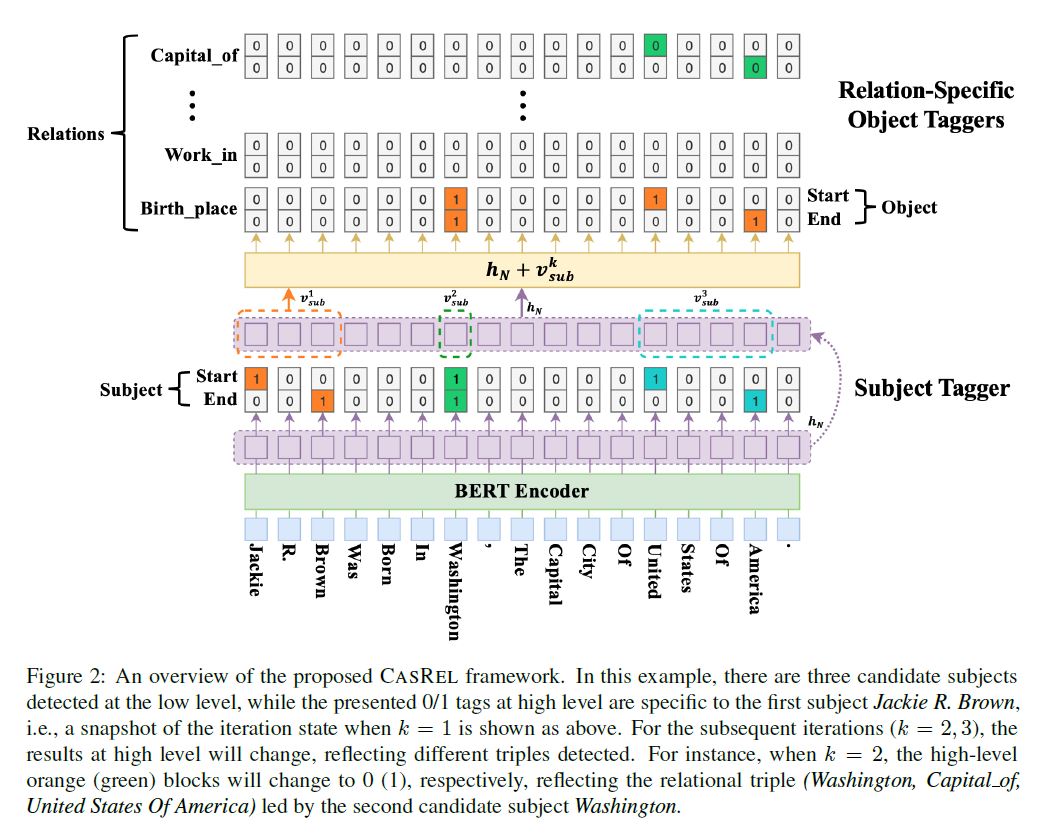
训练目标
针对训练集 $D$ 中的句子$x_j$,给定对应的潜在overlap triples集合 $ T_j = \{(s,r,o)\} $,最大化数据似然估计:
$ \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{(s,r,o) \in T_j} {p((s,r,o)|x_j)}\right]} $
$ = \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{s \in T_j} p(s|x_j) \prod\limits_{(r,o) \in T_j|s} p((r,o)|s,x_j)\right]}$
$ = \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{s \in T_j} p(s|x_j) \prod\limits_{ r \in T_j|s} p_r(o|s,x_j) \prod\limits_{r \in R \backslash T_j|s} p_r(o_{\emptyset}|s,x_j)\right]}$
其中,$s \in T_j$ 表示出现在 $T_j$ 中三元组的主体(subject),
$T_j | s $ 表示 $T_j$ 中主体是 $s$ 的三元组集合,
$R$ 是所有可能的关系的集合,
$\backslash$ 表示集合的差集,
$o_\emptyset$ 表示”null”客体。
对于任一个给定的主体 s , 在”s确实参与表达的关系r”的作用下,必定可以映射为客体 o ,而对于其他关系,映射为”空”客体 $null$
BERT Encoder
编码器使用Bert
Subject Tagger
训练两个二元分类器,分别识别Subject的开始位置和结束位置,标识为1, 其他标识为0
对于每一个起始位置,从该位置依次向后寻找最近的结束位置, 从而寻找出所有Subject
$p_i^{start_s} = \sigma (W_{start} X_i + b_{start})$,
$p_i^{end_s} = \sigma (W_{end} X_i + b_{end})$,
$ X_i $ 表示序列第i个词的bert编码,
$\sigma $ 表示sigmoid激活函数。
loss
最大化似然函数:
$p_\theta(s|X) = \prod\limits_{t \in \{start_s,end_s\}} {\prod\limits_{i=1}^L (p_i^t)^{I\{y_i^t = 1\} }(1-p_i^t)^{I\{y_i^t = 0\}}}$,
$L$是句子长度,
$I\{z\} = 1$ ,如果 z 为 true, 否则 0,
$\theta$ 是参数集合
经过这一步骤,可是识别出句子中所有Subject
Relation-specific Object Taggers
针对每一个关系 $r$,训练两个二元分类器,分别识别针对关系r映射出的Object的开始位置和结束位置,标识为1, 否则标识为0
$p_i^{start_o} = \sigma (W_{start}^r (X_i + V^k_{sub}) + b_{start}^r)$,
$p_i^{end_o} = \sigma (W_{end}^r (X_i + V^k_{sub}) + b_{end}^r)$,
$V_{sub}^k$ 表示subject tagger识别出的第k个Subject的编码,若为多个词构成,取均值
loss
最大化似然函数:
$p_{\emptyset_r}(o|s, X) = \prod\limits_{t \in \{start_o,end_o\}} {\prod\limits_{i=1}^L (p_i^t)^{I\{y_i^t = 1\} }(1-p_i^t)^{I\{y_i^t = 0\}}}$,
$L$是句子长度,
$I\{z\} = 1$ ,如果 z 为 true, 否则 0,
$\emptyset_r$ 是参数集合,
另外,“空”客体Object,意味着
针对Subject Tagger识别出的每一个Subject,计算该subject在每个关系作用下的Object。
对于每一个关系 $r$
若得到非空Object,既可以抽取出关系三元组,
若得到空Object,则认为不存在该关系。
整体Loss
最大化似然函数:
$J(\Theta) = \sum\limits _{j=1} ^ {|D|} \left[ {\sum\limits _{s \in T_j} \log p_\theta(s|X_j)} + {\sum\limits _{r \in T_j|s} \log p_{\emptyset_r}(o|s,X_j)} + {\sum\limits _{r \in R \backslash T_j|s} \log p_{\emptyset_r}(o_\emptyset|s,X_j)} \right]$