摘要
远程监督由于其强烈的假设,深受噪音数据标签的影响。
大多数现有工作都在bag级别采用选择性注意力机制来降噪。
但是其无法胜任单句子bag的情况。本文提出:
- 提出一种实体感知词嵌入方法(entity-aware word embedding),来整合位置信息和头/尾实体embedding,以突出此任务的实体本质;
- 以PCNN捕获局部依存关系,并提出一种自注意力机制(self-attention)来捕获全局依存关系,作为PCNN的补充;
- 设计一个基于池的门(pooling-equipped gate),来代替选择性注意力机制,该门基于上下文表示,作为聚合器生成bag级别的表示。
与选择性注意力机制相比,该门控机制的主要优点是,即使bag中只有一个句子,也可以稳定执行,从而在所有训练数据中保持一致。
在NYT 2010数据集上实验表明,该模型在AUC和top-n指标方面均达到SOTA性能。
拟解决的问题
- 单句子bag在实际数据集上占比很高,并且单句子bag的标签很可能是错误的,即噪音bag;
- 单句子bag的情况,会迫使基于选择性注意力机制的模型,返回单值标量的权重,导致注意力模块不能充分训练,从而影响性能。
创新点
- 使用实体嵌入(entity embedding)和相对位置嵌入(position embedding),并提出一种实体感知嵌入方法(entity-aware embedding approach)将实体信息动态集成到每个单词嵌入中,产生更具表达力的表示;
- 为增强PCNN捕获长期依赖的能力(Yu等人,2018),开发一种轻量级的自注意机制来捕获丰富的依赖信息,为PCNN产生互补依赖表示;
- 设计一个选择性门结构(selective gate),将句子级别表示聚合为bag级别的表示。
Model
(注: 本人认为本篇论文中的公式描述和模型图片都有点错误)
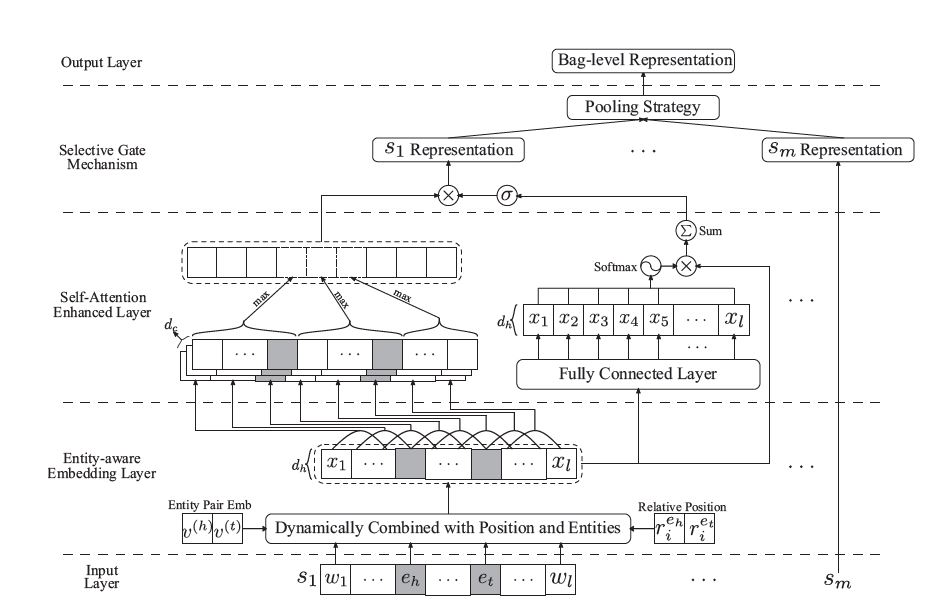
Entity-Aware Embedding
计算过程如下:
1.首先针对bag中的每一个句子:
$s= [\omega_1,\omega_2,…,\omega_n]$, 词嵌入表示为 $X^{(\omega)} = [v_1,v_2,…,v_n] \in R^{d_\omega \times n}$
2.加入相对位置嵌入(相对距离), 位置嵌入表示为 $ r_i^{e_h} 、r_i^{e_t} \in R^{d_r}$:
$ X^{(p)} = [x_1^{(p)}, x_2^{(p)},…,x_n^{(p)}] \in R^{d_p \times n} , \forall x_i^{(p)} = [v_i; r_i^{e_h}; r_i^{e_t}], 其中d_p = d_\omega + 2 \times d_r$
3.加入实体嵌入, 头尾实体嵌入表示为$v^{(h)}、v^{(t)}$:
$X^{(e)} = [x_1^{(e)}, x_2^{(e)},…,x_n^{(e)}] \in R^{3d_\omega \times n}, \forall x_i^{(e)} = [v_i; v^{(h)};v^{(t)}] \in R^{3d_\omega}$
4.gate机制计算:
$ \alpha=sigmoid(\lambda \cdot (W^{(g1)}X^{(e)} + b^{(g1)})) \in R^{d_h \times n}, W^{(g1)} \in R^{d_h \times 3d_\omega}, \lambda是超参数$
$\tilde{X}^{(p)} = \tanh(W^{(g2)}X^{(p)} + b^{(g2)}) \in R^{d_h \times n}, W^{(g2)} \in R^{d_h \times d_p}$
$X =\alpha \cdot (W^{(X)} X^{(e)}+ b^{(X)}) + (1-\alpha) \cdot \tilde X ^{(p)} \in R^{d_h \times n}, 其中W^{(X)} \in R^{d_h \times 3d_\omega}$
得到的$X$,被认为是所有单词的entity-aware embedding。
self-Attention Enhanced Neural Network
之前的一些工作(Vaswani等人,2017)发现,CNN由于缺乏衡量长期依赖的能力,即使堆叠多层,也无法在大多数NLP Benchmarks上达到SOTA性能。
PCNN
针对每一个句子的计算公式
一维卷积操作可以表示为:
$ H^{(c)} = 1D_CNN(X;W^{(c)}; b^{(c)}) \in R^{d_c \times n}, d_c是输出通道个数(卷积核个数)$
所得output根据头尾实体位置划分:
$H^{(c)} = [H^{(1)},H^{(2)},H^{(3)}]$
$s = \tanh([Pool(H^{(1)}); Pool(H^{(2)}); Pool(H^{(3)})]) \in R^{3d_c}$
Self-Attention Mechanism
计算公式:
$A = W^{(\alpha2)} \sigma(W^{(\alpha1)}X + b^{(\alpha1)}) + b^{(\alpha2)}, 其中W^{(\alpha1)}、W^{(\alpha2)} \in R^{d_h \times d_h}, \sigma 是激活函数$
$P^{(A)} = softmax(A) \in R^{d_h \times n}$
$u = \sum P^{(A)} \odot X \in R^{d_h}$
Selective Gate
给定一个包含m个句子的bag,通过PCNN、Self-Attention得到的句子表示为
$S = [s_1,s_2,…,s_m] \in R^{3d_c \times m}$, $U = [u_1,u_2,…,u_m] \in R^{d_h \times m}$
计算公式如下:
1.首先逐句生成gate值,该值控制该句子的表示是否应该被保留
$g_j = sigmoid(W^{(g1)} \sigma(W^{(g2)}u_j + b^{(g2)}) + b^{(g1)}) \in R^{3d_c}, \forall j=1,…,m$
$W^{(g1)} \in R^{3d_c \times d_h}, W^{(g2)} \in R^{d_h \times d_h} , \sigma(\cdot)是激活函数$
2.对PCNN的句子表示加权求和
$c = \frac 1 m \sum_{j=1}^m {g_j \cdot s_j} \in R^{3d_c}$
Output
$p = softmax(MLP(c)) \in R^{|C|}, 其中|C|是关系种类$
LOSS
L2正则化
$L_{NLL} = - \frac 1 {|D|} \sum_{k=1}^{|D|} \log p_{(y^k)}^k + \beta || {\theta} || _2^2, 其中\theta表示模型所有参数,\beta是系数$