git push项目到github：

1
2
3
4
5
6
7
8
9
10
11

git init

git add .

git commit -m "first commit"

git branch -M main

git remote add origin git@github.com:RidongHan/xxx.git

git push origin main

其他命令

1
2
3

git status

git reflog

git-lfs 大文件支持

1

git lfs track "*.zip"

最大频率降为70%

1

echo "70" | sudo tee /sys/devices/system/cpu/intel_pstate/max_perf_pct

查看效果

1

watch -n 0 "cat /proc/cpuinfo | grep -i mhz"

dpkg强制卸载软件，忽略依赖warning

1

sudo dpkg --purge --force-depends 软件名

例如：

1

sudo dpkg --purge --force-depends "libglvnd-dev"

摘要

在关系抽取中，远程监督引起两个主要挑战：

• 错误标签
• 长尾关系（NYT数据集中，41个关系类别（共53个）只有不到1000个训练样例）

最近的工作通过“多实例学习的选择性注意力”减轻错误标签影响，

但即使引入关系的层次结构来共享知识，也不能很好地处理长尾关系。

为解决上述问题，本文提出一种新的神经网络，即协作关系增强的注意力（Collaborating Relation-augmented Attention，CoRA）。

具体如下：

• 首先提出关系增强注意力网络(relation-augmented attention network)，作为 base model。
  • bag级别的sentence-to-relation注意力机制，最大程度减少错误标记的影响。
• 基于 base model，引入在关系的层次结构中，各关系间共享的协同特征（collaborating relation features）
  • 促进关系增强过程
  • 平衡长尾关系的训练数据

主要训练目标:

• 预测句子bag的关系

辅助目标：

• 指导关系增强过程，以获得更准确的bag级特征表示

CoRA在数据集NYT上进行的实验在 $Precision@N$，$AUC$ 和 $Hits@K$ 指标上均达到SOTA。

对比实验的进一步分析也证明了CoRA在处理长尾关系方面的卓越能力。

引言

在关系抽取中，远程监督引起两个主要挑战：

• 错误标签
• 长尾关系（NYT数据集中，41个关系类别（共53个）只有不到1000个训练样例）

1. 对于错误标签问题：

最近的工作大多是通过“多实例学习的选择性注意力”减轻错误标签影响

1. 对于long-tail问题：

摘要

本文拟解决基于 “带有不可靠标签的数据” 训练神经网络的问题。

基于假设观察到的标签是真实标签的带噪观测结果，从而引入一个额外的噪音层，模拟噪音分布对真实标签的影响。

• 提出一种同时学习神经网络参数和噪声分布的方法
• 在几个标准分类任务上的对比实验说明了该方法对性能的提升。
• 在某些情况下，即使“人工手动标注并假定没有错误的数据”，该方法也有所帮助。

模型

假设在训练过程中不能直接观察到正确标签y，只能观察到带噪标签z

噪音分布可以看作关系标签间的转移概率

$\theta (i,j) = p(z=j|y=i) $

观测的带噪标签 z 的概率：

$ p(z=j|x;\omega, \theta) = \sum\limits_{i=1}^k p(z=j|y=i; \theta) p(y=i|x;\omega), $

$\omega是参数集合, x是输入特征（可以是句子、手工创建的特征等）, k是关系的个数$

模型结构图如下：

model

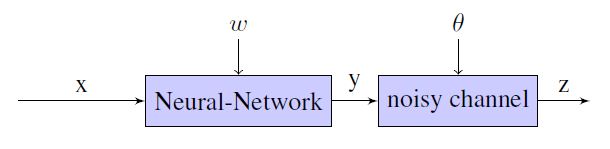
对于输入特征 $x$ , 编码后的特征向量表示为 $h = h(x)$,

$p(y=i|x;\omega) = \frac {\exp(u_i^\top h)}{\sum\limits_{j=1}^k \exp(u_j^\top h)}, i=1,2,…,k$

$u$ 是参数

训练阶段

给定 n 个输入特征 $x_1,…,x_n$, 相对应的观测带噪标签 $z_1,…, z_n$ , 真实标签 $y_1,…,y_n$

对数极大似然估计：

$L(\omega, \theta) = \sum\limits_{t=1}^n \log (\sum\limits_{i=1}^k p(z_t|y_t=i;\theta) p(y_t=i|x_t;\omega))$

目标是：最大化该似然函数，找出参数 $\omega$ 、噪音分布 $\theta$

由于

Improving Long-Tail Relation Extraction with Collaborating Relation-Augmented Attention

拟解决问题

远程监督关系抽取的标记噪音问题

出发点

提出”远程监督中，最终句子对齐的标签是基于某些未知因素所生成的带噪观测结果”这一假设。

模型

模型结构如下图所示：

带噪观测模型

摘要

现有工作很少能够较好地解决关系三元组的重叠问题（overlapping triple problem）。

本文用一个新的视角来重新审视关系提取任务，并提出了一种级联二分标注框架(Cascade Binary Tagging Framework, 简称CasRel)。

该框架将关系（relation）建模为主体（subject）与客体（object）的函数映射，而不是像以前的工作那样将关系视为离散标签。

实验表明，该框架在多个场景下均可以获得性能提升，某些场景大幅度超越现有SOTA。

拟解决问题

重叠三元组问题overlapping triple problem有以下三种情形：

本文方案

本文关系抽取任务定义

本文的框架将关系（relation）建模为主体（subject）与客体（object）的函数映射，而不是像以前的工作那样将关系视为离散标签。

由学习关系分类器（relation为离散关系标签）

$f(s,o) \to r$

转变为学习主体s在关系r下对客体o的函数映射

$f_r(s) \to o$

基于上述视角，关系抽取任务可以分为以下两个步骤：

• 确定句子中所有可能的主体 (subject)；
• 针对每个主体subject，使用特定于关系的标注器（relation-specific tagger）同时识别所有可能的关系和相应的客体object

CasRel框架（三部分）：

• BERT-based encoder module (基于Bert的编码器模块)

• subject tagging module(主体标注模块)

• relation-specific object tagging module(区分关系的客体标注模块)

模型结构

训练目标

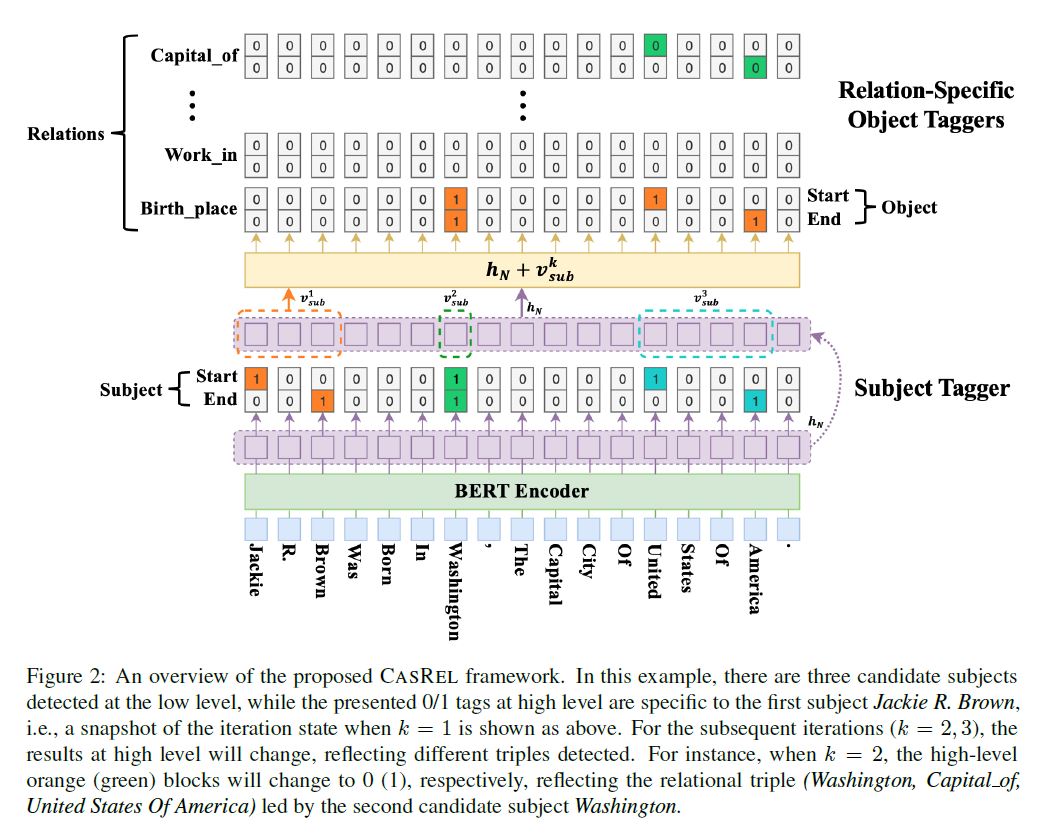
针对训练集 $D$ 中的句子$x_j$，给定对应的潜在overlap triples集合 $ T_j = \{(s,r,o)\} $，最大化数据似然估计：

$ \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{(s,r,o) \in T_j} {p((s,r,o)|x_j)}\right]} $

$ = \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{s \in T_j} p(s|x_j) \prod\limits_{(r,o) \in T_j|s} p((r,o)|s,x_j)\right]}$

$ = \prod\limits_{j=1}^{|D|} {\left[ \prod\limits_{s \in T_j} p(s|x_j) \prod\limits_{ r \in T_j|s} p_r(o|s,x_j) \prod\limits_{r \in R \backslash T_j|s} p_r(o_{\emptyset}|s,x_j)\right]}$

其中，$s \in T_j$ 表示出现在 $T_j$ 中三元组的主体（subject），

$T_j | s $ 表示 $T_j$ 中主体是 $s$ 的三元组集合，

$R$ 是所有可能的关系的集合，

$\backslash$ 表示集合的差集,

$o_\emptyset$ 表示”null”客体。

对于任一个给定的主体 s , 在”s确实参与表达的关系r”的作用下，必定可以映射为客体 o ,而对于其他关系，映射为”空”客体 $null$

BERT Encoder

编码器使用Bert

Subject Tagger

训练两个二元分类器，分别识别Subject的开始位置和结束位置,标识为1, 其他标识为0

对于每一个起始位置，从该位置依次向后寻找最近的结束位置, 从而寻找出所有Subject

$p_i^{start_s} = \sigma (W_{start} X_i + b_{start})$,

$p_i^{end_s} = \sigma (W_{end} X_i + b_{end})$,

$ X_i $ 表示序列第i个词的bert编码，

$\sigma $ 表示sigmoid激活函数。

loss

最大化似然函数：
$p_\theta(s|X) = \prod\limits_{t \in \{start_s,end_s\}} {\prod\limits_{i=1}^L (p_i^t)^{I\{y_i^t = 1\} }(1-p_i^t)^{I\{y_i^t = 0\}}}$,

$L$是句子长度，

$I\{z\} = 1$ ，如果 z 为 true， 否则 0，

$\theta$ 是参数集合

经过这一步骤，可是识别出句子中所有Subject

Relation-specific Object Taggers

针对每一个关系 $r$,训练两个二元分类器，分别识别针对关系r映射出的Object的开始位置和结束位置，标识为1， 否则标识为0

$p_i^{start_o} = \sigma (W_{start}^r (X_i + V^k_{sub}) + b_{start}^r)$,

$p_i^{end_o} = \sigma (W_{end}^r (X_i + V^k_{sub}) + b_{end}^r)$,

$V_{sub}^k$ 表示subject tagger识别出的第k个Subject的编码，若为多个词构成，取均值

loss

最大化似然函数：

$p_{\emptyset_r}(o|s, X) = \prod\limits_{t \in \{start_o,end_o\}} {\prod\limits_{i=1}^L (p_i^t)^{I\{y_i^t = 1\} }(1-p_i^t)^{I\{y_i^t = 0\}}}$,

$L$是句子长度，

$I\{z\} = 1$ ，如果 z 为 true， 否则 0，

$\emptyset_r$ 是参数集合,

另外，“空”客体Object，意味着

针对Subject Tagger识别出的每一个Subject，计算该subject在每个关系作用下的Object。
对于每一个关系 $r$
若得到非空Object，既可以抽取出关系三元组，
若得到空Object，则认为不存在该关系。

整体Loss

最大化似然函数：

$J(\Theta) = \sum\limits _{j=1} ^ {|D|} \left[ {\sum\limits _{s \in T_j} \log p_\theta(s|X_j)} + {\sum\limits _{r \in T_j|s} \log p_{\emptyset_r}(o|s,X_j)} + {\sum\limits _{r \in R \backslash T_j|s} \log p_{\emptyset_r}(o_\emptyset|s,X_j)} \right]$

主题模型 （Topic Model）

• 主题模型（Topic Model）是以无监督学习的方式对文档的隐含语义结构(latent semantic structure)进行聚类(clustering)的统计模型。

主题模型认为在词(word)与文档(document)之间没有直接的联系，应当还有一个维度将它们串联起来，这个维度称为主题(topic)。

每个文档都对应着一个或多个主题，而每个主题都有对应的词分布，通过主题，就可以得到每个文档的词分布。

由此有公式：

在一个已知的数据集中，词和文档对应的$p(\omega_i | d_j)$都是已知的。主题模型就是根据这个已知的信息，通过计算$p(\omega_i | t_k)$和$p( t_k | d_j)$，从而得到主题的词分布和文档的主题分布信息。

常用方法

• LSA（Latent Semantic Analysis）
  • 主要采用SVD（奇异值分解）暴力破解
• LDA（Latent Dirichlet Allocation, 隐含狄利克雷分布）
  • 贝叶斯学派方法论进行拟合

LSA（Latent Semantic Analysis）

LSA最初用在语义检索上，为解决一词多义和一义多词的问题：

• 一义多词：

  美女和PPMM表示相同的含义，但是单纯依靠检索词“美女”来检索文档，很可能丧失掉那些包含“PPMM”的文档。

• 一词多义：

  如果输入检索词是多个检索词组成的一个小document，例如“清澈 孩子”，那我们就知道这段文字主要想表达concept是和道德相关的，不应该将“春天到了，小河多么的清澈”这样的文本包含在内。

为了能够解决这个问题，需要将词语（term）中的concept提取出来，建立一个词语和概念的关联关系（t-c relationship），这样一个文档就能表示成为概念的向量。这样输入一段检索词之后，就可以先将检索词转换为概念，再通过概念去匹配文档

LDA (Latent Dirichlet Allocation)

隐含狄利克雷分布（Latent Dirichlet Allocation, LDA）是由David Blei等人在2003年提出的，该方法的理论基础是贝叶斯理论。

LDA根据词的共现信息，拟合出词-文档-主题的分布，进而将词、文本都映射到一个语义空间中。

LDA算法假设文档中主题的先验分布和主题中词的先验分布都服从狄利克雷分布。在贝叶斯学派看来，先验分布+数据(似然)=后验分布。我们通过对已有数据集的统计，就可以得到每篇文档中主题的多项式分布和每个主题对应词的多项式分布。然后就可以根据贝叶斯学派的方法，通过先验的狄利克雷分布和观测数据得到的多项式分布，得到一组Dirichlet-multi共轭，并据此来推断文档中主题的后验分布，也就是我们最后需要的结果。那么具体的LDA模型应当如何进行求解，其中一种主流的方法就是吉布斯采样。结合吉布斯采样的LDA模型训练过程一般如下：

随机初始化，对语料中每篇文档中的每个词w，随机地赋予一个topic编号z。
重新扫描语料库，对每个词w按照吉布斯采样公式重新采样它的topic，在语料中进行更新。
重复以上语料库的重新采样过程直到吉布斯采样收敛。
统计语料库的topic-word共现频率矩阵，该矩阵就是LDA的模型。
经过以上的步骤，就得到一个训练好的LDA模型，接下来就可以按照一定的方式针对新文档的topic进行预估，具体步骤如下：

随机初始化，对当前文档中的每个词w，随机地赋予一个topic编号z。
重新扫描当前文档，按照吉布斯采样公式，重新采样它的topic。
重复以上过程直到吉布斯采样收敛。
统计文档中的topic分布即为预估结果。

摘要

远程监督由于其强烈的假设，深受噪音数据标签的影响。

大多数现有工作都在bag级别采用选择性注意力机制来降噪。
但是其无法胜任单句子bag的情况。

本文提出：

• 提出一种实体感知词嵌入方法(entity-aware word embedding),来整合位置信息和头/尾实体embedding，以突出此任务的实体本质；
• 以PCNN捕获局部依存关系，并提出一种自注意力机制（self-attention）来捕获全局依存关系，作为PCNN的补充；
• 设计一个基于池的门(pooling-equipped gate)，来代替选择性注意力机制，该门基于上下文表示，作为聚合器生成bag级别的表示。

与选择性注意力机制相比，该门控机制的主要优点是，即使bag中只有一个句子，也可以稳定执行，从而在所有训练数据中保持一致。

在NYT 2010数据集上实验表明，该模型在AUC和top-n指标方面均达到SOTA性能。

拟解决的问题

• 单句子bag在实际数据集上占比很高，并且单句子bag的标签很可能是错误的，即噪音bag；
• 单句子bag的情况，会迫使基于选择性注意力机制的模型，返回单值标量的权重，导致注意力模块不能充分训练，从而影响性能。

创新点

• 使用实体嵌入(entity embedding)和相对位置嵌入(position embedding)，并提出一种实体感知嵌入方法(entity-aware embedding approach)将实体信息动态集成到每个单词嵌入中，产生更具表达力的表示;
• 为增强PCNN捕获长期依赖的能力（Yu等人，2018），开发一种轻量级的自注意机制来捕获丰富的依赖信息，为PCNN产生互补依赖表示;
• 设计一个选择性门结构（selective gate），将句子级别表示聚合为bag级别的表示。

Model

(注: 本人认为本篇论文中的公式描述和模型图片都有点错误)

结构图

Entity-Aware Embedding

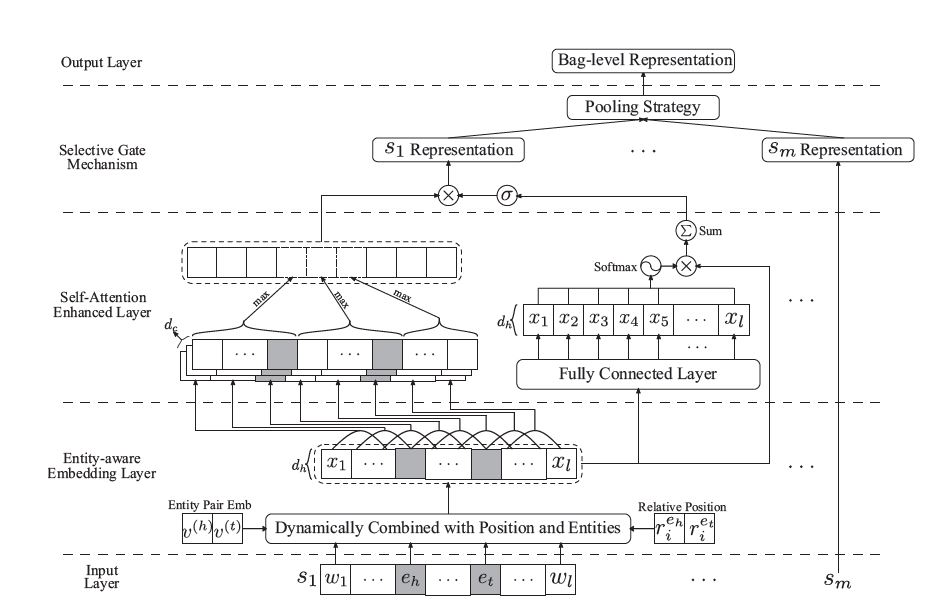
计算过程如下：

1.首先针对bag中的每一个句子：

$s= [\omega_1,\omega_2,…,\omega_n]$, 词嵌入表示为 $X^{(\omega)} = [v_1,v_2,…,v_n] \in R^{d_\omega \times n}$

2.加入相对位置嵌入(相对距离), 位置嵌入表示为 $ r_i^{e_h} 、r_i^{e_t} \in R^{d_r}$：

$ X^{(p)} = [x_1^{(p)}, x_2^{(p)},…,x_n^{(p)}] \in R^{d_p \times n} , \forall x_i^{(p)} = [v_i; r_i^{e_h}; r_i^{e_t}], 其中d_p = d_\omega + 2 \times d_r$

3.加入实体嵌入, 头尾实体嵌入表示为$v^{(h)}、v^{(t)}$：

$X^{(e)} = [x_1^{(e)}, x_2^{(e)},…,x_n^{(e)}] \in R^{3d_\omega \times n}, \forall x_i^{(e)} = [v_i; v^{(h)};v^{(t)}] \in R^{3d_\omega}$

4.gate机制计算：

$ \alpha=sigmoid(\lambda \cdot (W^{(g1)}X^{(e)} + b^{(g1)})) \in R^{d_h \times n}, W^{(g1)} \in R^{d_h \times 3d_\omega}, \lambda是超参数$

$\tilde{X}^{(p)} = \tanh(W^{(g2)}X^{(p)} + b^{(g2)}) \in R^{d_h \times n}, W^{(g2)} \in R^{d_h \times d_p}$

$X =\alpha \cdot (W^{(X)} X^{(e)}+ b^{(X)}) + (1-\alpha) \cdot \tilde X ^{(p)} \in R^{d_h \times n}, 其中W^{(X)} \in R^{d_h \times 3d_\omega}$

得到的$X$,被认为是所有单词的entity-aware embedding。

self-Attention Enhanced Neural Network

之前的一些工作（Vaswani等人，2017）发现，CNN由于缺乏衡量长期依赖的能力，即使堆叠多层，也无法在大多数NLP Benchmarks上达到SOTA性能。

PCNN

针对每一个句子的计算公式

一维卷积操作可以表示为：

$ H^{(c)} = 1D_CNN(X;W^{(c)}; b^{(c)}) \in R^{d_c \times n}, d_c是输出通道个数(卷积核个数)$

所得output根据头尾实体位置划分：

$H^{(c)} = [H^{(1)},H^{(2)},H^{(3)}]$

$s = \tanh([Pool(H^{(1)}); Pool(H^{(2)}); Pool(H^{(3)})]) \in R^{3d_c}$

Self-Attention Mechanism

计算公式:

$A = W^{(\alpha2)} \sigma(W^{(\alpha1)}X + b^{(\alpha1)}) + b^{(\alpha2)}, 其中W^{(\alpha1)}、W^{(\alpha2)} \in R^{d_h \times d_h}, \sigma 是激活函数$

$P^{(A)} = softmax(A) \in R^{d_h \times n}$

$u = \sum P^{(A)} \odot X \in R^{d_h}$

Selective Gate

给定一个包含m个句子的bag，通过PCNN、Self-Attention得到的句子表示为

$S = [s_1,s_2,…,s_m] \in R^{3d_c \times m}$, $U = [u_1,u_2,…,u_m] \in R^{d_h \times m}$

计算公式如下：

1.首先逐句生成gate值，该值控制该句子的表示是否应该被保留

$g_j = sigmoid(W^{(g1)} \sigma(W^{(g2)}u_j + b^{(g2)}) + b^{(g1)}) \in R^{3d_c}, \forall j=1,…,m$

$W^{(g1)} \in R^{3d_c \times d_h}, W^{(g2)} \in R^{d_h \times d_h} , \sigma(\cdot)是激活函数$

2.对PCNN的句子表示加权求和

$c = \frac 1 m \sum_{j=1}^m {g_j \cdot s_j} \in R^{3d_c}$

Output

$p = softmax(MLP(c)) \in R^{|C|}, 其中|C|是关系种类$

LOSS

L2正则化

$L_{NLL} = - \frac 1 {|D|} \sum_{k=1}^{|D|} \log p_{(y^k)}^k + \beta || {\theta} || _2^2, 其中\theta表示模型所有参数，\beta是系数$

摘要

最近远程监督关系抽取的NRE模型都是针对每个分包bag，通过学习句子的重要性权重来减轻不相关句子的影响。
目前为止，努力的重点是提高抽取的准确性，但对模型的解释性知之甚少。

本文标注了一个带有基本事实句子级解释的测试集，以评估关系提取模型提供的可解释性。
实验证明，用细粒度实体类型（entity type）替换句子中的实体不仅提高了提取的准确性，而且改善了可解释性。
本文还提出**自动生成“干扰”句子，对bag数据增强，并训练模型忽略这些“干扰”句子。
在FB-NYT数据集上，本文取得了SOTA性能，同时提高了模型可解释性。

引言

远程监督关系抽取降噪研究：

• 基于attention的模型
• 利用附加资源（additional resources）的模型
• 利用监督数据的模型

现有方法，关注于提高模型的准确率（accuracy），而对于模型是因为正确的推理还是某些不相关的偏置/偏见而正确分类知之甚少。

Baseline Models

DirectSup

给定一个分包bag，DirectSup使用具有不同过滤器大小的CNN对每个句子进行编码。
连接具有不同滤波器大小的CNN的输出，以产生句子的编码。

CNNs+ATT